'បញ្ហាទឹកពុះ' លើការប្រឡងថ្នាក់ទី១០ បង្កជម្លោះ

ទីក្រុងហូជីមិញ៖ បញ្ហាទឹកពុះ ក្នុងការប្រឡងគណិតវិទ្យា ថ្នាក់ទី១០ បង្កភាពចម្រូងចម្រាស ព្រោះវាចាត់ទុកថា ជារឿងមិនសមហេតុផល ក្នុងការពិត និងមិនត្រឹមត្រូវ លើចំណេះដឹងរូបវិទ្យា។

នៅថ្ងៃទី 6 និងទី 7 ខែមិថុនា បេក្ខជនជិត 96.000 នាក់បានប្រឡងអក្សរសាស្ត្រ ភាសាបរទេស និងគណិតវិទ្យា ដើម្បីប្រកួតប្រជែងដណ្តើមយកកន្លែងនៅក្នុងសាលារដ្ឋថ្នាក់ទី 10 ក្នុងទីក្រុងហូជីមិញ។ លោកគ្រូអ្នកគ្រូបានលើកឡើងថា ការប្រឡងគណិតវិទ្យាមានរចនាសម្ព័ន្ធ និងការលំបាកដូចឆ្នាំមុនដែរ។ ការប្រឡងមានបញ្ហាអនុវត្តចំនួន៥ ចាប់ពីសំណួរទី៣ ដល់សំណួរទី៧។

បន្ទាប់ពីការប្រឡងបានបញ្ចប់ លោក Mai Van Tuc គ្រូបង្រៀនរូបវិទ្យានៅវិទ្យាល័យ Gifted in Natural Sciences នៃសាកលវិទ្យាល័យជាតិហាណូយ បាននិយាយថា សំណួរទី 5 ក្នុងការប្រឡងគណិតវិទ្យាថ្នាក់ទី 10 នៅទីក្រុងហូជីមិញ បានបង្ហាញពីច្បាប់ដែលមិនមាននៅក្នុងការពិត និងខុសជាមូលដ្ឋាន។

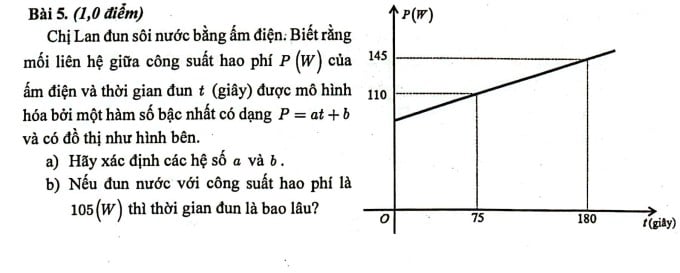
សំណួរទី៥ ក្នុងការប្រឡងគណិតវិទ្យា សម្រាប់ប្រឡងចូលសាលារដ្ឋ ថ្នាក់ទី១០ នៅទីក្រុងហូជីមិញ។

ជាពិសេសដំណើរការនៃការបំប្លែងថាមពលនៅពេលទឹករំពុះត្រូវបានគណនាចាប់ពីពេលដែលកុងតាក់ត្រូវបានបើក (នៅ t = 0); ថាមពលអគ្គិសនីត្រូវបានបំប្លែងទៅជាថាមពលកំដៅ ដែលធ្វើឱ្យខ្សែភ្លើងក្តៅ (ប្រសិនបើកំសៀវប្រើខ្សែកំដៅ)។ ខ្សែកំដៅមានសីតុណ្ហភាពខ្ពស់ជាងទឹកនៅក្នុងកំសៀវ ហើយផ្ទេរកំដៅទៅក្នុងទឹក ទឹកផ្ទេរកំដៅទៅកំសៀវ ហើយត្រូវចំណាយពេលមួយរយៈដើម្បីឱ្យកំដៅបាត់បង់ដល់បរិស្ថាន។ សមត្ថភាពបាត់បង់កំដៅដល់បរិស្ថានពឹងផ្អែកជាចម្បងលើតំបន់ទំនាក់ទំនងនៃកំសៀវជាមួយបរិស្ថាន និងភាពខុសគ្នានៃសីតុណ្ហភាពរវាងសីតុណ្ហភាពនៃកំសៀវ និងបរិស្ថាន (សមត្ថភាពបាត់បង់ក៏អាស្រ័យលើកម្រិតនៃចរន្តខ្យល់ ឬខ្យល់នៅកន្លែងកំដៅ)។ នៅពេលដែលសមត្ថភាពបាត់បង់កំដៅដល់បរិស្ថាននៃកំសៀវគឺស្មើនឹងថាមពលដែលបានទទួលដោយខ្សែកំដៅ សីតុណ្ហភាពនៃទឹកនឹងលែងកើនឡើងទៀតហើយ។

លោកគ្រូ ទុយ បានលើកឧទាហរណ៍អំពីខ្សែកំដៅដែលមានសមត្ថភាព 1,000 W. ប្រសិនបើទឹកដាំក្នុងកំសៀវ 2 លីត្រ ទឹកអាចឆ្អិនបាន ប៉ុន្តែប្រសិនបើខ្សែកំដៅនេះផ្តល់កំដៅដល់អាងចិញ្ចឹមត្រីធំ ទឹកអាចកំដៅត្រឹមតែ 10 អង្សាសេទៅ 30 អង្សាសេ នោះសីតុណ្ហភាពនឹងមិនកើនឡើងទៀតទេ។ នៅពេលនោះការបាត់បង់ថាមពលនៅតែថេរនិងស្មើនឹងការប្រើប្រាស់ថាមពលនៃខ្សែកំដៅនៃកំសៀវ។ ដូច្នេះសំណួរទី 5 ផ្តល់នូវការបាត់បង់ថាមពលយោងទៅតាមច្បាប់ P = at + b នោះគឺ t = 0 ការបាត់បង់ថាមពលស្មើនឹង 85 W ហើយការបាត់បង់ថាមពលកើនឡើងជាលំដាប់ដែលខុស។ គ្រូក៏គិតខុសដែរ ពេលសួរថា "បើទឹកស្ងោរបាត់បង់ថាមពល 105 W តើវាចំហុយដល់ពេលណា?"។ ប្រសិនបើយើងសន្មត់ថាមានច្បាប់មិនសមហេតុផលដូចអ្នកនិពន្ធផ្តល់ឱ្យនោះ យើងត្រូវសួរថា: គណនាពេលវេលាពុះរហូតដល់ការបាត់បង់ថាមពលគឺ 105 W ។

ជាមួយនឹងទឡ្ហីករណ៍ទាំងនេះ លោក Tuc បានស្នើឱ្យ មន្ទីរអប់រំ និងបណ្តុះបណ្តាលទីក្រុងហូជីមិញ កែសម្រួលចម្លើយចំពោះសំណួរទី 5 ដើម្បីធានាបាននូវភាពយុត្តិធម៌សម្រាប់បេក្ខជន។ គ្រូម្នាក់នេះជឿថា សិស្សដែលពូកែរូបវិទ្យា ប្រហែលជាមិនអាចធ្វើសំណួរទី៥បានទេ នៅពេលដែលទិន្នន័យក្នុងសំណួរចម្លែកពេក។

ទន្ទឹមនឹងនេះ លោក Lam Vu Cong Chinh គ្រូបង្រៀនគណិតវិទ្យានៅវិទ្យាល័យ Nguyen Du ទីក្រុងហូជីមិញ បាននិយាយថា ប្រសិនបើយើងពិចារណាលើចំណេះដឹងរូបវិទ្យា និងការពិត ទិន្នន័យនៅក្នុងសំណួរទី 5 មិនសមហេតុផល និងសមហេតុផលនោះទេ។ ទោះជាយ៉ាងណាក៏ដោយ ប្រសិនបើសំណួរគ្រាន់តែជាការស្ទង់មតិ សំយោគ និងផ្តល់រូបមន្តទស្សន៍ទាយ មិនមែនជារូបមន្តរូបវិទ្យាពិតប្រាកដទេ វានៅតែអាចទទួលយកបាន។

លោក Chinh បានលើកឧទាហរណ៍អំពីការប៉ាន់ប្រមាណកំណើនប្រជាជន។ យោងទៅតាមគាត់ នេះគឺជាបញ្ហាដែលមិនមានរូបមន្តត្រឹមត្រូវពិតប្រាកដនោះទេ ទោះជាយ៉ាងណាក៏ដោយ អ្នកជំនាញនៅតែអនុវត្តរូបមន្តមួយស្របតាមច្បាប់ និងការពិតមួយចំនួន ដើម្បីទស្សន៍ទាយ និងប៉ាន់ស្មានចំនួនប្រជាជននាពេលអនាគត។

លោក ឈិន បានមានប្រសាសន៍ថា “ប្រសិនបើសិស្សអនុវត្តចំណេះដឹងគណិតវិទ្យា ពួកគេនៅតែអាចដោះស្រាយបញ្ហាបានជាធម្មតា។ កំហុសនេះមិនប៉ះពាល់ដល់លទ្ធផលប្រឡងរបស់បេក្ខជននោះទេ។

អ្នកស្រី Nguyen Tien Thuy គ្រូបង្រៀនគណិតវិទ្យានៅអនុវិទ្យាល័យ Ha Huy Tap ទីក្រុងហូជីមិញ បានអត្ថាធិប្បាយថា សំណួរទី 5 គឺស្ថិតក្នុងទម្រង់នៃមុខងារកម្រិតទីមួយ។ សំណួរផ្តល់រូបមន្តសម្រាប់អនុគមន៍ដឺក្រេទី 1 ជាមួយនឹងរូបមន្តច្បាស់លាស់សម្រាប់បរិមាណ និងឯកតានីមួយៗ រួមជាមួយនឹងរូបភាពក្រាហ្វិក ដូច្នេះសិស្សអាចដោះស្រាយវាបានជាធម្មតា។

បេក្ខជនសំណេះសំណាលក្រោយការប្រឡងគណិតវិទ្យា ព្រឹកថ្ងៃទី៧ ខែមិថុនា។ រូបភាព៖ Le Nguyen — បេក្ខជនសំណេះសំណាលក្រោយការប្រឡងគណិតវិទ្យានៅព្រឹកថ្ងៃទី៧ មិថុនា។ រូបភាព *៖ ឡេង ង្វៀន*

នាថ្ងៃទី ៩ មិថុនា មន្ទីរអប់រំ និងបណ្តុះបណ្តាលទីក្រុងហូជីមិញ បានឲ្យដឹងថា សំណួរទី៥ នៃការប្រឡងគណិតវិទ្យាថ្នាក់ទី១០ រួមមានខ្លឹមសារទាក់ទងនឹងបាតុភូតពិតនៃដំណើរការដាំទឹកក្នុងកំសៀវអគ្គិសនី។ ដំណើរការស្ទង់មតិនេះគ្រាន់តែជាដំណាក់កាលខ្លីនៃដំណើរការស្រូបទឹក ហើយពេលវេលាដែលការស្ទង់មតិបានចាប់ផ្តើម (t=0) មិនមែនជាពេលដែលដំណើរការស្រូបទឹកចាប់ផ្តើមនោះទេ។

ជាមួយនឹងទិន្នន័យដែលបានស្ទង់មតិនៅក្នុងដំណើរការនេះ គណិតវិទ្យាអាចពិពណ៌នាថាជាគំនូរ និងដោយមុខងារដែលសិស្សបានរៀននៅក្នុងកម្មវិធី។ ដូច្នេះជាមួយនឹងចំណេះដឹង និងសមត្ថភាពគណិតវិទ្យា (អនុគមន៍ដឺក្រេទីមួយ ក្រាហ្វនៃអនុគមន៍ដឺក្រេទីមួយ ចំណុចនៅលើក្រាហ្វ ប្រព័ន្ធនៃសមីការដឺក្រេទី 1 ដែលមានពីរមិនស្គាល់ ការគណនា) សិស្សអាចដោះស្រាយតម្រូវការដែលបានកំណត់ដោយបញ្ហា។

នាយកដ្ឋានព័ត៌មានបាននិយាយថា "ក្នុងករណីដែលសិស្សមានដំណោះស្រាយខុសពីការណែនាំអំពីចំណាត់ថ្នាក់ ប៉ុន្តែសមហេតុផល ពួកគេនឹងត្រូវបានគេពិចារណា និងវាយតម្លៃ"។

កាលពីឆ្នាំមុន ប្រហែល 45% នៃបេក្ខជនប្រឡងចូលរៀនថ្នាក់ទី 10 នៅទីក្រុងហូជីមិញ ទទួលបានពិន្ទុទាបជាងមធ្យមភាគផ្នែកគណិតវិទ្យា។

ឆ្នាំនេះ ទីក្រុងហូជីមិញមានសិស្សប្រមាណ ៩៦.០០០ នាក់កំពុងប្រឡងចូលថ្នាក់ទី ១០ នៅសាលារដ្ឋ។ គោលដៅចុះឈ្មោះចូលរៀនសរុបសម្រាប់វិទ្យាល័យសាធារណៈចំនួន 108 របស់ទីក្រុងគឺ 77,300 ជាមួយនឹងអត្រាចូលរៀនប្រហែល 80% ។ នាយកដ្ឋានអប់រំ និងបណ្ដុះបណ្ដាលបានឲ្យដឹងថា ពិន្ទុប្រឡងនឹងត្រូវប្រកាសនៅថ្ងៃទី ២០ ខែមិថុនា។

ឡេង ង្វៀន

ប្រភពតំណ