Существует ли вид «немыслящей» математики?
Доктор Нгуен Фи Ле (факультет информационных и коммуникационных технологий Ханойского университета науки и технологий) когда-то хорошо учился по математике, завоевав серебряную медаль на международном математическом конкурсе IMO 2000 года, при этом ему не приходилось брать слишком много дополнительных занятий. Поэтому, когда его ребёнок ещё учился в начальной школе, доктор Ле не считал, что ему нужны дополнительные занятия по математике вообще и по «мыслительной математике» в частности, хотя в то время на рынке репетиторских услуг появилось множество центров, предлагающих обучение «мыслительной математике». Однако, когда его ребёнок учился в пятом классе и позже сдавал вступительные экзамены в десятый класс, доктор Ле был вынужден разрешить ему посещать дополнительные занятия по математике, поскольку только так он мог сдать вступительные экзамены в специализированные школы и классы по выбору.

Многие родители позволяют своим детям осваивать математическое мышление с раннего возраста, надеясь, что их дети преуспеют в математике.
Например, недавно, после вступительного экзамена в 10-й класс по математике в Высшей школе естественных наук Университета естественных наук Вьетнамского национального университета в Ханое, преподаватели и студенты много обсуждали один геометрический вопрос. Хороший преподаватель, специализирующийся на преподавании геометрии, сказал, что сидел и решал этот вопрос 3-4 часа. Однако ученику 9-го класса нужно было решить его за короткое время. Если ученик не ходил на пробные экзамены и никогда не решал подобные задачи, он точно не сможет сдать этот экзамен. Даже ученик с очень хорошими мыслительными способностями не сможет…
«Выполняйте очень сложное упражнение в необычном формате за короткое время. Чтобы выполнить такое упражнение, нужно много времени», — поделился доктор Ле.
Доктор Ле также сказала, что, видя, что её ребёнок слишком много посещает дополнительные занятия, она посоветовала ему больше времени уделять самостоятельным занятиям, потому что только тогда мозг ученика успеет усвоить знания, что поможет ему стать самостоятельным и в дальнейшем быть самостоятельным при решении задач. Однако ребёнок не успокоился, опасаясь, что не сможет соревноваться с друзьями в гонке, где сильнее были ученики, усердно занимавшиеся на занятиях по подготовке к экзаменам.
По словам профессора Ле Ань Винь, директора Вьетнамского института педагогических наук, многие математики испытывают аллергию, когда кто-то говорит «мыслительная математика». Разве это означает, что существует «немыслящая математика»? Но реальность такова, что современные методы обучения математике предполагают множество способов, которые не учат мышлению, а лишь учат счёту. На занятиях учителя зачастую учат учеников выполнять упражнения по моделям (что часто называют «математикой по форме»). При таком методе обучения, решив определённый тип математической задачи, ученики часто выполняют её очень быстро, совершенно не задумываясь.
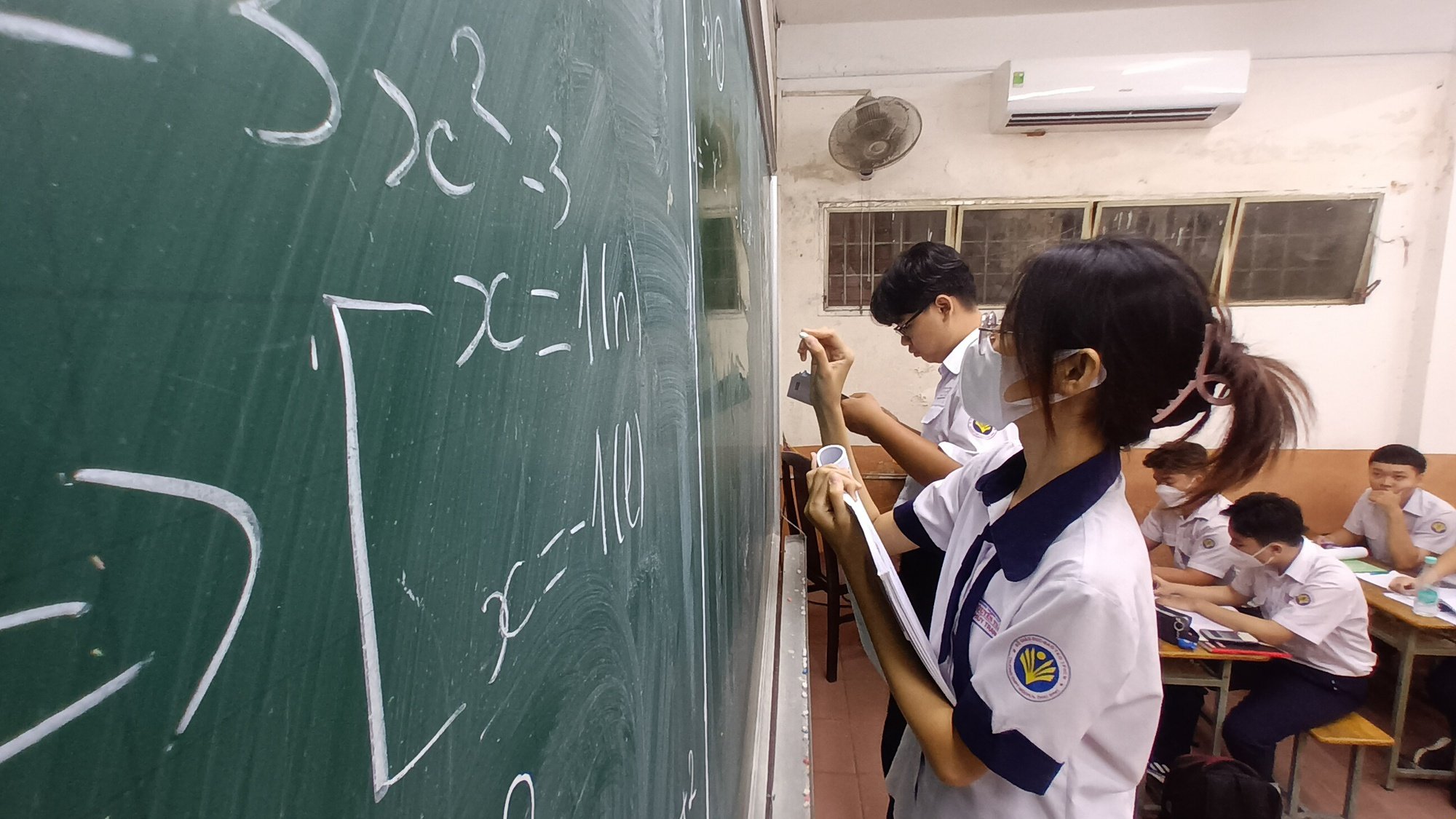
Новая общеобразовательная программа делает акцент на математике, связанной с практикой, с применением, с решением вопроса, для чего нужна математика, а не просто с выполнением упражнений.
КОГДА ИЗУЧЕНИЕ МАТЕМАТИКИ БОЛЬШЕ НЕ ЯВЛЯЕТСЯ ПРИРОДОЙ ИЗУЧЕНИЯ МАТЕМАТИКИ
По словам доктора Ву Тхи Нгок Ха из Института прикладной математики и информатики Ханойского университета науки и технологий, каждый научный предмет способствует развитию и совершенствованию мышления у каждого ребенка, люди называют это «разнообразием фундаментальных областей», а не только изучение математики для развития мышления.
Однако в математике задачи всегда связаны с реальностью. Чтобы преодолеть это, ребёнок должен пройти через этапы построения задачи на основе анализа законов природы, а затем, используя логическое и творческое мышление, решить её. При этом иногда для решения задачи задействуются воображение и критическое мышление.
«Математика сама по себе, по-видимому, является предметом, который лучше всего стимулирует мышление. Поэтому рождение центров «математического мышления» вполне объяснимо в нынешней ситуации, когда перед нами стоит задача освоить определённый модуль знаний по каждому предмету, и не только по математике, в очень короткие сроки, чтобы подготовиться к экзаменам. Это создаёт способ изучения математики, который больше не соответствует природе «изучения математики», — прокомментировал доктор Нгок Ха.
Профессор Ле Ань Винь рассказал, что поначалу у него тоже была аллергия на выражение «мыслящая математика». Позже, после исследования, выяснилось, что преподавание математики без размышлений всё ещё довольно популярно. Профессор Винь прокомментировал: «Если мы говорим, что здесь мы преподаём математику, а не учим математике без размышлений, это звучит слишком натянуто. Поэтому, когда кто-то или где-то представляется как преподаватель мысленной математики, это означает, что он преподаёт математику в истинном смысле этого слова. Таким образом, «мыслящая математика» исходит из того, что люди хотят преподавать математику так, чтобы ученики думали и могли применять её в жизни, а не просто в форме, чтобы ученики получали действительно высокие баллы на экзаменах. Родителям тоже стоит задуматься, потому что, когда они представляются таким образом, это означает, что они учат учеников не тому, как учить математику для успешной сдачи экзаменов, а тому, как думать».
C НЕОБХОДИМОСТЬ ИННОВАЦИОННОЙ СИСТЕМЫ ЭКЗАМЕНОВ
Доктор Нгок Ха считает, что для того, чтобы изучение математики вернулось к своей истинной природе, ученикам необходимо «учиться медленно», поскольку «медленное обучение» — это самый совершенный способ стимулировать развитие мышления каждого ребенка.
Столкнувшись с проблемой, ученики должны иметь время (очень много времени) на выявление природных явлений, затем на поиск величин и законов, на установление взаимосвязей между величинами посредством выражений, а затем на поиск методических инструментов для решения задачи. Таким образом, создать программу под названием «думающая математика» очень сложно. Но преподавание ещё сложнее, поскольку помимо умения «медленно-медленно» учитель должен обладать общими знаниями на высоком уровне. Обучение должно быть гибким и соответствовать качествам и способностям каждого ученика. Это очень сложно, когда ребёнок находится под давлением академических достижений, оценок и ожиданий родителей, ограничивая своё время...
Научите УЧАЩИХСЯ думать, а не считать.
Профессор Ле Ань Винь часто в шутку говорит учителям математики: научить учеников думать 10 минут сложнее, чем научить их сидеть и считать час. Если в школе просто получить рабочий лист, сесть и считать как можно быстрее и качественнее, то после занятий в головах учеников ничего не останется. Сталкиваясь с новыми ситуациями, ученики не умеют думать, не могут применять полученные знания для решения задач. Однако это системная проблема, характерная для экзаменов, контрольных и упражнений, из-за которой люди пропускают все этапы развития мышления, сосредотачиваясь только на том, чтобы научить учеников считать и выполнять упражнения.
В частности, преподавание математики как обучения мышлению требует синхронизации всей системы: программы, учебников, времени каждого часа, каждой минуты, каждого предмета, системы экзаменов, социальной психологии...

Абитуриенты 9-го класса в Хошимине в аудитории, где проходил вступительный экзамен по математике в 10-й класс. На экзамене было много практических задач.
По словам профессора Виня, новая общеобразовательная программа делает акцент на математике, связанной с практикой, с применением, с решением вопроса, для чего нужна математика, а не просто с выполнением упражнений.
Доктор Фи Ле сказала, что поддерживает студентов, посещающих дополнительные занятия по предметам, которые им интересны и по которым они способны, но таким образом, чтобы это развивало их творческие способности и мыслительные способности. Посещение дополнительных занятий в форме подготовки к экзаменам в нынешнем виде не очень полезно для студентов. «Проблема в том, что при нынешней формулировке вопросов студенты, никогда не изучавшие типы вопросов на экзамене, становятся „лузерами“. В нынешней экзаменационной среде существует неравная конкуренция между студентами, которые учатся „думать“, и студентами, которые учатся готовиться к экзаменам. Обдумывание занимает много времени, и приходится идти на риск не знать многих типов вопросов. Именно эта „мотивация“ заставляет студентов „вынужденно“ посещать дополнительные занятия».
«Как же проводить экзамены, чтобы развивать мышление учащихся? Вопросы экзамена не должны быть сложными, должны соответствовать материалу общеобразовательных школ и выявлять учащихся с хорошими навыками мышления», — сказал доктор Фи Ле.
Ссылка на источник





![[Фото] Премьер-министр Фам Минь Чинь председательствует на заседании Постоянного комитета Правительственного партийного комитета](https://vstatic.vietnam.vn/vietnam/resource/IMAGE/2025/8/23/8e94aa3d26424d1ab1528c3e4bbacc45)


![[Фото] Генеральный секретарь То Лам принимает участие в праздновании 80-летия традиционного Дня сектора культуры](https://vstatic.vietnam.vn/vietnam/resource/IMAGE/2025/8/23/7a88e6b58502490aa153adf8f0eec2b2)





































































Комментарий (0)